Probabilistic Modeling Examples¶
This gallery contains advanced examples of probabilistic geological modeling and Bayesian geophysical inversion using GemPy with Pyro probabilistic programming.
Gallery Overview¶
These examples demonstrate uncertainty quantification and probabilistic inference methods for geological and geophysical problems. They leverage PyTorch and Pyro to perform:
Uncertainty propagation through geological models
Bayesian inversion of geophysical data
Joint inversion of multiple data types
Posterior sampling and credible interval estimation
Why Probabilistic Modeling?¶
Traditional deterministic geological models provide a single “best guess” interpretation. Probabilistic modeling offers several advantages:
Quantifies uncertainty: Provides probability distributions over model parameters
Incorporates prior knowledge: Combines geological expertise with data
Rigorous inference: Uses Bayesian statistics for optimal parameter estimation
Risk assessment: Enables decision-making under uncertainty for resource exploration
Prerequisites¶
Completion of Basic Examples gallery
Understanding of probability and statistics
Familiarity with Bayesian inference concepts (helpful but not required)
Installed packages:
gempy,gempy-probability,pyro-ppl,torch,arviz
Example Descriptions¶
02_error_propagation.py: Propagate uncertainty in surface point locations through a geological model to understand how data uncertainty affects predictions
03_error_propagation_dips.py: Extend uncertainty analysis to orientation data, demonstrating the impact of dip and azimuth uncertainties
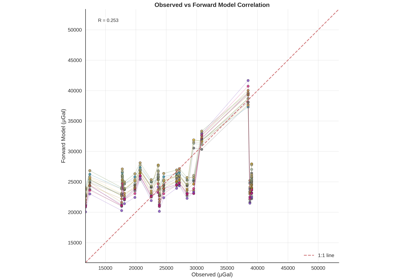
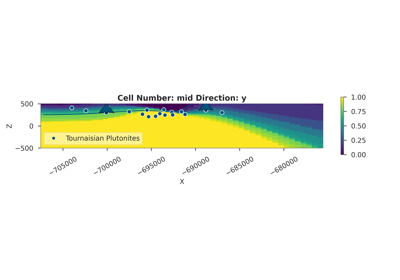
04_gravity_inversion.py: Full Bayesian inversion of gravity data to infer subsurface density distributions and geological parameters
05_magnetics_inversion.py: Magnetic data inversion demonstrating joint geophysical-geological inference
06_enmap_inversion.py: Surface lithology inversion using EnMap satellite classifications with Categorical likelihood and ordinal probabilities
07_joint_inversion.py: Joint Bayesian inversion of gravity and EnMap data, demonstrating multi-grid setup and likelihood balance diagnostics
Inference Methods¶
These examples use two main inference approaches:
Variational Inference (VI):
Fast approximate inference using gradient descent
Suitable for large-scale problems
Provides mean-field or structured approximations
Markov Chain Monte Carlo (MCMC):
Accurate sampling from posterior distributions
Slower but more robust
Uses Hamiltonian Monte Carlo (HMC) and NUTS algorithms
Computational Requirements¶
Probabilistic modeling is computationally intensive:
Expect runtime of minutes to hours depending on problem size
GPU acceleration recommended for large inversions
Some examples save pre-computed results (
arviz_data_*.ncfiles)
Visualization and Diagnostics¶
All examples use ArviZ for posterior analysis:
Trace plots to check convergence
Posterior distributions and credible intervals
Effective sample size and \(\\hat{R}\) diagnostics
Posterior predictive checks
See also
Pyro Documentation - Probabilistic programming framework
ArviZ - Exploratory analysis of Bayesian models
GemPy-Probability - Integration layer
Note
Some examples may take significant time to run. Pre-computed results are provided where possible to enable quick visualization without re-running full inversions.
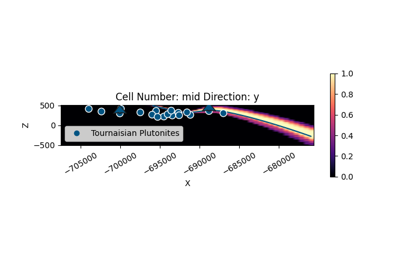
Bayesian Magnetic Inversion: TMI Inversion Workflow
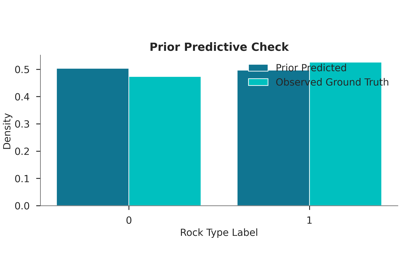
Bayesian EnMap Inversion: Categorical Likelihood and Ordinal Probabilities